Un conjunto es una colección bien definida de objetos, entendiendo que dichos objetos pueden ser cualquier cosa: números, personas, letras, otros conjuntos, etc. Algunos ejemplos son:
- A es el conjunto de los números naturales menores que 5.
- B es el conjunto de los colores verde, blanco y rojo.
- C es el conjunto de las vocales a, e, i, o y u.
- D es el conjunto de los palos de la baraja francesa.
Los conjuntos se denotan habitualmente por letras mayúsculas. Los objetos que componen el conjunto se llaman elementos o miembros. Se dice que «pertenecen» al conjunto y se denota mediante el símbolo ∈:[n 1] la expresión a ∈ A se lee entonces como «a está en A», «a pertenece a A», «A contiene aa», etc. Para la noción contraria se usa el símbolo ∉. Por ejemplo:
- 3 ∈ A , ♠ ∈ D
- amarillo ∉ B, z ∉ C
Notación

Relación de pertenencia. El conjunto A es un conjunto de polígonos. En la imagen, algunas de las figuras pertenecen a dicho conjunto, pero otras no.
Existen varias maneras de referirse a un conjunto. En el ejemplo anterior, para los conjuntos A y D se usa una definición intensiva o por comprensión, donde se especifica una propiedad que todos sus elementos poseen. Sin embargo, para los conjuntos B y C se usa una definición extensiva, listando todos sus elementos explícitamente.
Es habitual usar llaves para escribir los elementos de un conjunto, de modo que:
- B = {verde, blanco, rojo}
- C = {a, e, i, o, u}
Esta notación mediante llaves también se utiliza cuando los conjuntos se especifican de forma intensiva mediante una propiedad:
- A = {Números naturales menores que 5}
- D = {Palos de la baraja francesa}
Otra notación habitual para denotar por comprensión es:
- A = {m : m es un número natural, y 1 ≤ m ≤ 5}
- D = {p : p es un palo de la baraja francesa}
- F = {n2 : n es un entero y 1 ≤ n ≤ 10},
En estas expresiones los dos puntos («:») significan «tal que». Así, el conjunto F es el conjunto de «los números de la forma n2 tal que n es un número natural entre 1 y 10 (ambos inclusive)», o sea, el conjunto de los diez primeros cuadrados de números naturales. En lugar de los dos puntos se utiliza también la barra vertical («|») u oblicua«/» .
Igualdad de conjuntos

Conjunto de personas. El conjunto de «personas» mostrado en la imagen, A, tiene 8miembros. Este conjunto puede representarse mediante llaves o mediante un diagrama de Venn. El orden de las personas en A es irrelevante.
Un conjunto está totalmente determinado por sus elementos. Por ello, la igualdad de conjuntos se establece como:
Esta propiedad tiene varias consecuencias. Un mismo conjunto puede especificarse de muchas maneras distintas, en particular extensivas o intensivas. Por ejemplo, el conjunto A de los números naturales menores que 5 es el mismo conjunto que A′, el conjunto de los números 1, 2, 3 y 4. También:
- B = {verde, blanco, rojo} = {colores de la bandera de México}
- C = {a, e, i, o, u} = {vocales del español}
- D = {Palos de la baraja francesa} = {♠, ♣, ♥, ♦}
El orden en el que se precisan los elementos tampoco se tiene en cuenta para comparar dos conjuntos:
- B = {verde, blanco, rojo} = {rojo, verde, blanco}
- C = {a, e, i, o, u} = {e, i, u, a, o}
Además, un conjunto no puede tener elementos «repetidos», ya que un objeto solo puede o bien ser un elemento de dicho conjunto o no serlo. Se da entonces que, por ejemplo:
- {1, 2} = {1, 2, 1}
En ausencia de alguna característica adicional que distinga los «1» repetidos, lo único que puede decirse del conjunto de la derecha es que «1» es uno de sus elementos.
Conjunto vacío
El conjunto que no contiene ningún elemento se llama el conjunto vacío y se denota por ∅o simplemente {}. Algunas teorías axiomáticas de conjuntos aseguran que el conjunto vacío existe incluyendo un axioma del conjunto vacío. En otras teorías, su existencia puede deducirse. Muchas posibles propiedades de conjuntos son trivialmente válidas para el conjunto vacío.
Propiedades
En la teoría de conjuntos axiomáticaestándar, por el Axioma de extenionalidad, dos conjuntos son iguales si tienen los mismos elementos; por lo tanto sólo puede haber un conjunto sin ningún elemento. Por consiguiente, sólo hay un único conjunto vacío, y hablamos de "el conjunto vacío" en lugar de "un conjunto vacío".
Para cualquier conjunto A:
- El conjunto vacío es un subconjunto de A:
- La unión de A con el conjunto vacío es A:
- La intersección de A con el conjunto vacío es el conjunto vacío:
- El producto cartesiano de A y el conjunto vacío es el conjunto vacío:
El conjunto vacío tiene las siguientes propiedades:
- Su único subconjunto es el propio conjunto vacío:
- El "conjunto de poder" del conjunto vacío es el conjunto que contiene únicamente el conjunto vacío:
- Su número de elementos (cardinalidad) es cero:
- (La lista de símbolos matemáticos empleados se encuentra aquí).
Subconjuntos
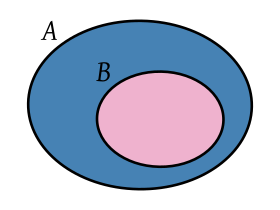
Un subconjunto A de un conjunto B, es un conjunto que contiene algunos de los elementos de B (o quizá todos):
Cuando A es un subconjunto de B, se denota como A ⊆ B y se dice que «A está contenido en B». También puede escribirse B ⊇ A, y decirse que B es un superconjunto de A y también «B contiene a A» o «B incluye a A».
Todo conjunto A es un subconjunto de sí mismo, ya que siempre se cumple que «cada elemento de A es a su vez un elemento de A». Es habitual establecer una distinción más fina mediante el concepto de subconjunto propio: A es un subconjunto propio de B si es un subconjunto de B pero no es igual a B. Se denota como A ⊊ B, es decir: A ⊆ B pero A ≠ B(y equivalentemente, para un superconjunto propio, B ⊋ A).[n 2]
Ejemplos.
- El «conjunto de todos los hombres» es un subconjunto propio del «conjunto de todas las personas».
- {1, 3} ⊊ {1, 2, 3, 4}
- {1, 2, 3, 4} ⊆ {1, 2, 3, 4}
Conjuntos disjuntos
Dos conjuntos A y B son disjuntos si no tienen ningún elemento en común. Por ejemplo, los conjuntos de los números racionales y los números irracionales son disjuntos: no hay ningún número que sea a la vez racional e irracional. La intersección de dos conjuntos disjuntos es el conjunto vacío